Пошук в ширину та глибину
Розглянемо алгоритм пошуку в графі зв'язку між вершинами А та В.
Створюємо чергу перегляду вершин. У чергу заносимо вершину А. Паралельно формуємо список переглянутих вершин.
Переглядаємо нашу чергу вершин і дописуємо в цю чергу всі вершини, з якими з'єднана та, яку зараз розглядаємо. Таким чином, ми додаємо в чергу вершини доти, поки не переберемо всі зв'язані вершини. Якщо у процесі ми знайдемо вершину В, то пошук можна завершити.

Паралельно нам потрібно відслідковувати з якої саме попередньої вершини ми побачили (занесли в чергу) поточну вершину - це буде список seenFrom.
g={}
g[0]=[1,3]
g[1]=[0,2,3,4]
g[2]=[1,3,4]
g[3]=[0,1,2]
g[4]=[1,2]
a=0
b=6
cherga=[]
cherga.append(a)
seenFrom=[n]*n
seenFrom[a]=a
while cherga:
if b not in cherga:
k=cherga.pop(0)
else:
break
for i in g1[k]:
cherga.append(i)
if seenFrom[i]==n:
seenFrom[i]=k
# роздрук шляху до вершини зі списку seenFrom
print(b) # друк кінцевої вершини
while seenFrom[b]!=b: # поки значення вершини не рівне її назві
print(seenFrom[b]) # друкуємо значення вершини (це вершина, з якої ми побачили цю)
b=seenFrom[b] # переходимо до вершини, з якої побачили цю
Такий пошук називається пошуком у ширину, бо ми переглядаємо вершини послідовно, від початкової точки до кожної, з якою ця точка має зв'язок. Якщо початкова точка не має зв'язку з кінцевою, значить переглядаємо нащадків початкової точки, і вершини, з якими вони зв'язані. І так доти, поки не дійдемо до шуканої вершини, або не вичерпаємо всі зв'язки.
До точки В можна дістатись й іншими шляхами. Наприклад, пошуком у глибину.

Він передбачає використання такої структури даних, як стек. Розглядаємо вершину та всі її зв'язки. Рухаємось за першим із поданих зв'язків доки не натрапимо на тупик. Тоді повертаємось на 1 крок назад і пробуємо рухатись знову до тупика.
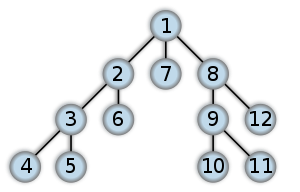
g1={0: [1, 3], 1: [0, 2, 3, 54], 2: [1, 3, 4], 3: [0,1, 2], 4: [1, 2]}
n=5
stek=[]
stek.append(a)
seen=[False]*n
seen[a]=True
while stek and seen[b]==False: # поки не завершаться вершини або поки не досягнемо потрібної
k=stek[len(stek)-1] #беремо останній елемент стеку
if len(g1[k])>0: #якщо до цього елемента ще є зв'язки
x=g1[k].pop(0) #вилучаємо перший зв'язок цього елемента
if seen[x]==False: #якщо його ще не розглядали
stek.append(x) #додаємо до стеку
seen[x]=True #і позначаємо розглянутим
elif len(g1[k])==0: # якщо в елемента більше немає зв'язків
stek.pop() # вилучаємо елемент зі стеку, це фактично повернення на крок назад
print(stek)
Завдання. Для заданого графу реалізувати алгоритм пошуку в ширину та глибину між вершинами 0 та 6

{0: [1, 2, 3], 1: [0, 2, 4, 5], 2: [0, 1, 3, 4], 3: [0, 2], 4: [1, 2, 6], 5: [1, 6], 6: [4, 5]}
0 1 1 1 0 0 0
1 0 1 0 1 1 0
1 1 0 1 1 0 0
1 0 1 0 0 0 0
0 1 1 0 0 0 1
0 1 0 0 0 0 1
0 0 0 0 1 1 0
Завдання. Намалюйте власний граф і випробуйте алгоритми пошуку в ширину та глибину для цього графа. Створіть анімацію пояснення процесу.
