Структури даних. Графи

Граф - це набір вершин та зв'язків між ними (ребер). Інформацію про граф можна зберігати у таблиці суміжності.

Необхідність визначити наявність зв'язку між двома вершинами виникає у таких задачах:

• У фотографіях - виділити область одного кольору
  
• Мережі - чи є зв’язок між комп’ютерами
  
• Соцмережі - друзі друзів, спільні друзі
  
• Провідність - чи пройде сигнал
  
• Вода - чи пройде через систему перешкод
  

У простих випадках  відповідь очевидна, але в серединному випадку проблема стає досить складною.

 Граф можна задавати графічно або за допомогою матриці чи списку суміжності.

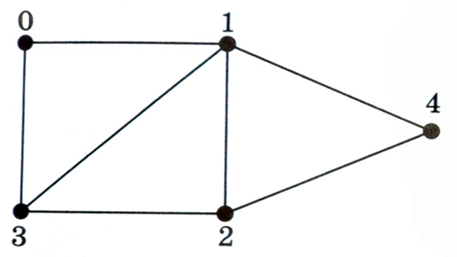
Наприклад, цей граф задано наступним описом:
Вершина 0 зв'язана з 1 і 3; 1 - з 0, 2, 3, 4; 2 - з 1 та 3; 3 - з 0, 1, 2, а 4 - з 1 та 2.

У програмі це можна задати у вигляді словника, ключами якого є вершини графа, а записами словника - списки вершин, з якими є зв'язки.

g={}
g[1]=[2,4]
g[2]=[1,3,4,5]
g[3]=[2,4,5]
g[4]=[1,2,3]
g[5]=[2,3]
print(g)

За цим словником можна сформувати двовимірний список, або матрицю суміжності:

gt = [[0]*n for i in range(n)] # створюємо порожню матрицю, заповнену нулями
for el in g1: # для кожного елемента словника
    for k in g1[el]: # перебираємо список, який відповідає цьому елементу
        gt[el][k]=1 # записуємо одиниці в матрицю суміжності на перетині рядка та стовпця зі списку
# для друку матриці:
for i in range(n):
    print()
    for j in range(n):
        print(gt[i][j], end=" ")

Зворотня задача (перетворення матриці суміжності на список суміжності),

gs={} # порожній словник
for i in range(n): # для кожного рядка матриці
    gs[i]=[] # номер рядка стає ключем словника
    for j in range(n): # для кожного стовпця у рядку
        if gt1[i][j]==1: # якщо значення у клітинці рівне 1
            gs[i].append(j) # дописуємо номер цього стовпця у словник
print(gs)

Задача 1. Простий орієнтовний граф задано у вигляді списків суміжності. Виведіть його подання у вигляді матриці суміжності.

https://www.e-olymp.com/uk/problems/3982

Вхідні дані 
У першому рядку міститься кількість вершин n (1 ≤ n ≤ 100). Далі йдуть n рядків. В i-му рядку міститься опис усіх ребер, які виходять з i-ої вершини. Опис розпочинається кількістю ребер, які виходять з вершин. Далі йдуть номери вершин, у які ці ребра йдуть. Усі вершини нумеруються натуральними числами від 1 до n.
3
2 2 3
0
1 2
Вихідні дані 
Виведіть матрицю суміжності орієнтовного графа.
0 1 1
0 0 0
0 1 0

Показати код/Сховати код^

Задача 2. Простий орієнтовний граф задано матрицею суміжності. Виведіть його подання у вигляді списків суміжності.

https://www.e-olymp.com/uk/problems/3981

Вхідні дані. 
У першому рядку знаходиться кількість вершин графа n (1 ≤ n ≤ 100). Далі йде матриця суміжності. Гарантується, що граф не містить петель.
5
0 0 1 0 0
1 0 1 0 0
0 0 0 0 1
1 1 0 0 0
1 1 0 0 0
Вихідні дані 
Виведіть n рядків - списки суміжності графа. В i-му рядку спочатку виведіть кількість ребер, які виходять з i-ої вершини, а потім номери вершин, у які ці ребра входять, впорядковані за зростанням.
1 3
2 1 3
1 5
2 1 2
2 1 2

Показати код/Сховати код^

Задача 3. У галактиці "Milky Way" на планеті "Neptune" є N міст, деякі з яких з'єднані дорогами. Імператор "Maximus" галактики "Milky Way" вирішив провести інвентаризацію доріг на планеті "Neptune". Але, як виявилось, він не дуже добре знає математику, тому він просить вас порахувати кількість доріг.

https://www.e-olymp.com/uk/problems/992

Вхідні дані
У першому рядку записано число N (0 ≤ N ≤ 100). У наступних N рядках записано по N чисел, кожне з яких є або одиничкою або нуликом. Причому, якщо у позиції (i, j) квадратної матриці стоїть одиничка, то i-те та j-те міста з'єднані дорогами, а якщо нулик, то не з'єднані.
5
0 1 0 0 0 
1 0 1 1 0 
0 1 0 0 0 
0 1 0 0 0 
0 0 0 0 0

Вихідні дані
Вивести одне число - кількість доріг на планеті "Neptune".
3

Показати код/Сховати код^

Задача 4. Знайти сумарну довжину доріг на планеті "Neptune".

5
0 2 3 4 0
2 0 5 0 7
3 6 0 8 0
0 0 0 0 0
0 7 0 9 0
Відповідь:
44

Показати код/Сховати код^

Існують й інші способи та інструменти роботи з графами: https://compucademy.co.uk/graphs-in-python-for-a-level-computer-science/