Структури даних. Масив та зв'язний список

Пам'ять комп'ютера

Спробуйте уявити собі пам'ять комп'ютера як шафу з пронумерованими комірками. У кожній комірці можна розмістити лише один предмет. 

Кожна комірка має певну адресу, наприклад:

Якщо потрібно здати на зберігання кілька предметів – виділяється кілька комірок. І спосіб вибору цих комірок може бути різним: у вигляді масиву (поряд) чи у вигляді зв’язного списку (з посиланням на наступну комірку).

Розглянемо масив, у якому всі елементи мають бути записані підряд у комірках пам'яті:

І припустимо, що хотіли би додати ще одну справу, але не можна – наступна комірка вже занята! Доведеться шукати вільний блок пам'яті, де зможуть розміститись всі елементи нашого набору даних. Тобто, додати елемент до масиву – це досить складний процес. Рішенням проблеми може бути завбачливе бронювання великого блоку пам'яті «про всяк випадок», проте це означає неефективне використання ресурсів, та й немає гарантії, що все-ж не доведеться збільшувати й цей розмір набору.

Дещо інакше працюють зв'язні списки, у яких елементи можуть мати довільне розміщення у пам'яті.

 

По суті, у кожній клітинці зберігається власний вміст та посилання на адресу наступного елемента списку. Таким чином, набір довільних адрес у пам'яті об'єднується в ланцюжок.

 

Це нагадує такий собі квест – приходимо за першою адресою і виявляємо записку «Наступний елемент знаходиться за адресою 123», приходимо туди і бачимо «Наступний елемент знаходиться за адресою 847» і т.д. Додати ще один елемент у зв'язний список не складає труднощів. Це також означає більш ефективне використання пам'яті, адже іноді неможливо знайти блок 10000 суміжних порожніх комірок, хоча загалом в пам'яті є 10000 вільних комірок, просто не підряд.

Водночас, зв'язний список має й певні недоліки: якщо потрібно побачити, наприклад, сьомий елемент списку, маємо пройти всі шість попередніх, адже ми не знаємо, у якій комірці буде той сьомий елемент. З масивами це зробити простіше, адже якщо блок пам'яті починається з певної адреси, то сьомий елемент розміщений у сьомій за порядком комірці після неї.

Таким чином, відмінність роботи масивів та зв'язних списків полягає у різному часі роботи двох типових операцій: читання та додавання елементів.

Для масиву читання = O(1), а додавання елемента = O. Для зв'язних списків – навпаки: читання = O, а додавання = O(1).

Якщо потрібно вставити елемент всередину набору, то зв'язний список буде ефективнішим.

 

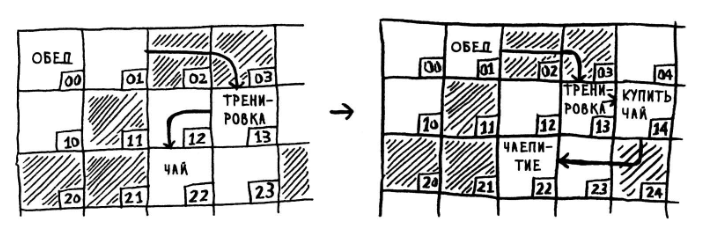
У випадку з масивом доведеться зміщувати елемент, а можливо навіть весь масив, якщо поряд не буде вільного місця.

 

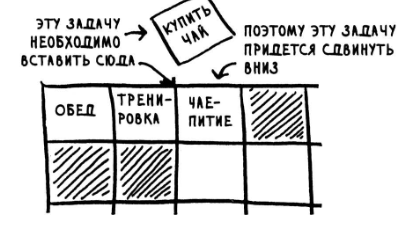
При видаленні елемента зв'язний список, знову ж, буде ефективнішим, адже потрібно буде лише змінити посилання між елементами. Тоді як у масиві – доведеться зміщувати всі наступні елементи. Але видалення, хоча би, завжди можливе, на відміну від вставки, яку може обмежити обсяг та конфігурація вільного місця.

У різних ситуаціях краще підходять різні структури. Буває, що їх варто поєднувати, наприклад:

 

В такому разі можна швидко знайти список всіх імен на певну літеру, і тоді вже перебирати всі імена послідовно. При цьому додавання та видалення елементів зі списків буде досить швидке, а проблема збільшення розміру масиву зникає за рахунок того, що кількість літер – обмежена і не мінятиметься впродовж роботи програми.

Списки в Python

У Python значно зручніше використовувати структуру списку, з якою ми вже досить багато працювали.

      

lost = [4,8,15,16,23,42]

for number in lost:

    print(number)

print(lost[2:5]) #надрукуємо список [15, 16, 23], тобто список елементів з індексами від 2 по 5 (5 не включно)

print(lost[3:]) #надрукуємо список [16, 23, 42], тобто список елементів з індексами від 3 до кінця

print(lost[:3]) #надрукуємо список [4, 8, 15], тобто список елементів з індексами від 0 по 3 (3 не включно)

Елемент списку можна замінити lost[2]=10

Додаємо елемент в кінець списку lost.append(100)

Елемент списку можна видалити del lost[3] #вказується індекс елемента, який треба видалити

Можна видаляти останній елемент списку lost.pop() та перший lost.pop(0)

Задача. Створити трикутник Паскаля

        1

      1   1

    1   2   1

  1   3   3   1

1   4   6   4   1

У формі списку він має такий вигляд: 

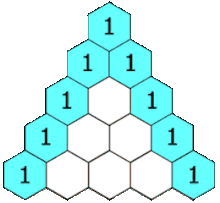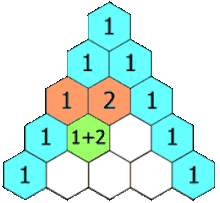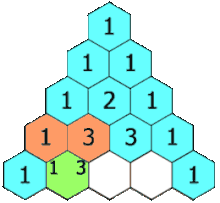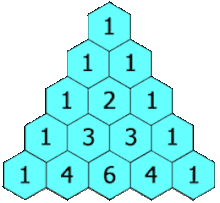
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

Цікаве про трикутник Паскаля: http://teoria0432.blogspot.com/2017/02/blog-post_24.html

pascal=[1]
pascal.append(1)
print(pascal)
for z in range(10):
    for k in range(len(pascal)-1):
        if k==0:
            pnew=[1]
        a=pascal[k+1]+pascal[k]
        pnew.append(a)
    pnew.append(1)
    pascal=pnew
    print(pascal)