Складність алгоритмів
За скільки операцій можна створити сітку на аркуші паперу?
Залежно від обраної стратегії, алгоритму рішення - можна це завдання виконувати швидше або повільніше.
Наприклад, можна малювати квадратики по одному. Можна провести певну кількість ліній горизонтально та вертикально - і з їх перетину утворяться квадрати. Можна складати аркуш паперу удвічі, знову удвічі і т.д. доки не отримаємо квадрати.
Іншими словами - ці алгоритми можуть мати різну ефективність. Чому це важливо? Перегляньте історію Алана Тюринга (http://moviestape.net/katalog_filmiv/drama/6934-gra-v-mtacyu.html, зокрема з 1:13:30 до 1:18:00) - тоді, як неефективний алгоритм не встигав виконати задачу розшифрування повідомлення за добу (а шифр змінювався щоразу опівночі), ефективніший алгоритм завершував розшифрування значно швидше, що давало змогу оперативно відреагувати на дії супротивника.
Ефективність та складність алгоритмів позначається великою літерою О, а в дужках вказується кількість операцій, які доведеться виконати для цього алгоритму.
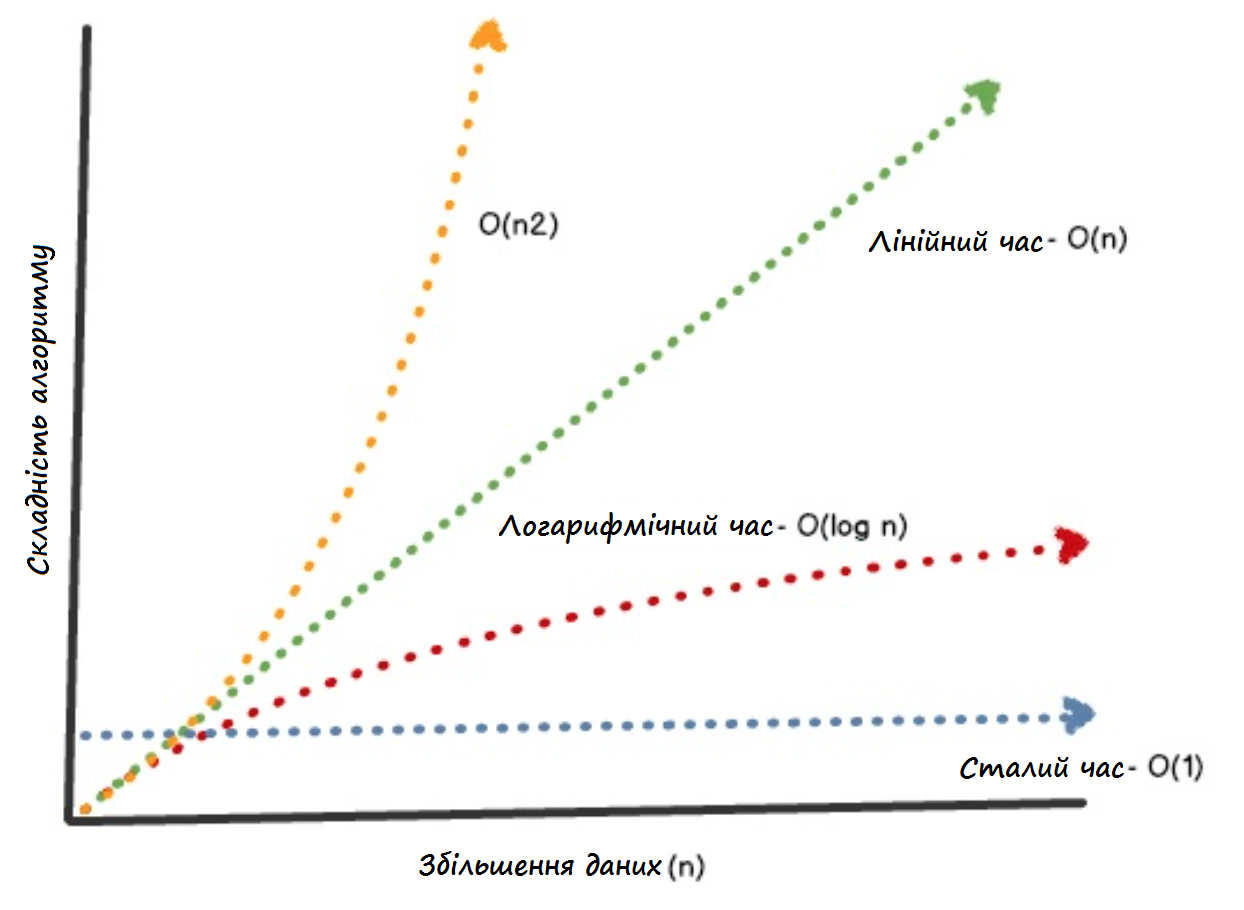
Різні алгоритми мають різні характеристики ефективності, найчастіше це одне із наступних значень:
O (log n) - приклад: бінарний пошук
O ( n ) - приклад: простий пошук
O (n*log n) - приклад: швидке сортування
O (n2) - приклад: сортування вибором
O (n!) - приклад: задача про комівояжера
Якщо за секунду можна виконати 10 операцій з обробки об'єктів, то алгоритми, в яких потрібно обробити 1024 об'єкти матимуть наступний час виконання:
O (log n) - 10 операцій = 1 секунда
O ( n ) - 1024 операції = 1,7 секунд
O (n*log n) - 17 хвилин
O (n2) - 1,2 доби
O (n!) - 5,4*102633 років
Повторення методів сортування: https://dystosvita.org.ua/mod/page/view.php?id=717Бінарний пошук - складність O(log n)
Припустимо, нам потрібно щось знайти в телефонній книзі (або в словнику) на літеру "К". Можна розпочати із першої сторінки і поступово рухатись до К. А можна відкрити книгу приблизно посередині, і таким чином швидше дійти до потрібного місця.
Аналогічна ситуація виникає тоді, коли ми, наприклад, входимо в обліковий запис соціальної мережі: сервер має перевірити, чи такий обліковий запис є у базі даних. Для цього необхідно виконати пошук: за алфавітом, чи, можливо, також розпочати з середини списку.
Згадаємо також задачу з вгадування числа комп'ютером: можна перебирати всі числа підряд з початку діапазону:
Проте варто використати стратегію пошуку середини діапазону і, відштовхуючись від результату - переходити до першої чи другої половини цього діапазону для генерування наступного припущення.
В усіх цих випадках доцільніше скористатись так званим бінарним пошуком, алгоритм якого полягає у наступному. На вході маємо впорядковану послідовність елементів. Якщо шуканий елемент присутній у списку, то на виході отримаємо його порядковий номер, інакше отримаємо null. За рахунок відкидання половини можливих варіантів на кожному із кроків алгоритму, ми дуже швидко отримаємо потрібний результат. Так, у словнику зі 100 елементів ми гарантовано отримаємо результат за 7 кроків:
Тобто, у найгіршому варіанті, цей алгоритм триватиме лише 7 кроків.
А тепер спробуємо визначити, скільки кроків алгоритму знадобиться для більшої кількості елементів, наприклад 240 тисяч записів.
Простий перебір у найгіршому варіанті займе 240 тисяч кроків. А бінарний пошук - всього 18 кроків!
У загальному випадку, для списку з n елементів, простий пошук триватиме n кроків, а бінарний - log2n кроків.
Логарифм - це операція, зворотня до підняття до степеня: log28 = 3, бо 2 у третій степені це 8.
Отож, для списку з 8 чисел у гіршому випадку простого пошуку доведеться перебрати 8 чисел, а бінарного пошуку - лише 3 числа. Для списку з 1024 елементів - це 1024 числа і 10 чисел відповідно.
Таким чином, простий пошук має лінійний час виконання, він збігається з розміром списку. Бінарний пошук має логарифмічний час виконання, це означає значну економію ресурсів при великій кількості елементів списку.
- Чи працюватиме бінарний пошук на невпорядкованій послідовності елементів?
- Якщо послідовність збільшити удвічі, як змінюється час пошуку?
Припустимо, перевірка одного елемента займає 1 мілісекунду. Якщо елементів 100, то лінійний час - це 100 мілісекунд, а логарифмічний - 7 мілісекунд. Якщо елементів мільярд, то логарифмічний пошук займе 30 мілісекунд, тоді як лінійний - 1 мільярд мілісекунд, що дорівнює 11 дням! Алгоритм не просто ефективніший, зокрема на малій кількості елементів, але його час виконання зростає надзвичайно повільно при збільшенні розміру списку.
Оскільки ця характеристика дуже важлива для оцінки ефективності алгоритмів, прийняте спеціальне позначення - О велике. В дужках записується кількість кроків цього алгоритму:
O ( n ) - ефективність алгоритму лінійного пошуку
O (log n) - ефективність алгоритму бінарного пошуку
Розглянемо реалізацію алгоритму бінарного пошуку на Python:
def binary_search(list, item):
# нижня та верхня межі пошуку
low = 0
high = len(list) - 1
# Поки ми не звузили пошук до єдиного елемента
while low <= high:
# перевіримо середину діапазону
mid = (low + high) // 2
guess = list[mid]
# Знайшли
if guess == item:
return mid
# Забагато
if guess > item:
high = mid - 1
# Замало
else:
low = mid + 1
# Елемента немає у списку
return None
# Протестуємо функцію
my_list = [1, 3, 5, 7, 9]
print binary_search(my_list, 3) # => 1
# 'None' позначає відсутність Python - ми це використовуємо, щоб позначити, що елемента немає у списку.
print binary_search(my_list, -1) # => None
Варто зауважити, що O описує найгірший випадок роботи алгоритму. Наприклад, може бути, що потрібно знайти слово на літеру А, і його буде знайдено дуже швидко при простому пошуку. Але пошук слова на літеру Я займе значно більше часу, тому запис О враховує найгірший варіант.
Сортування вибором O(n2)
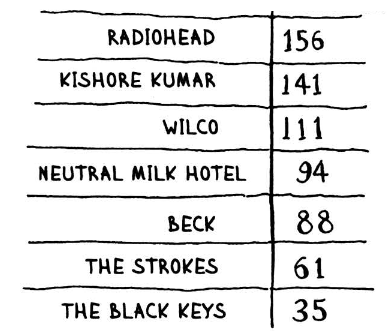
Розглянемо алгоритм, який виконує сортування, звертаючи увагу на ефективність його роботи. Наприклад, маємо наступний набір даних, з якого потрібно побудувати рейтинг улюблених виконавців.
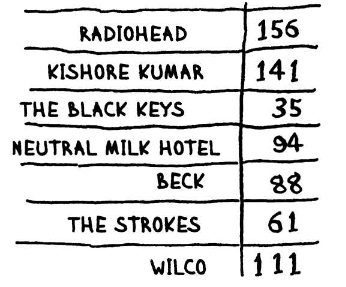
Одна із стратегій сортування може полягати у пошуку найбільшого елемента (за лічильником прослухувань) і встановленні його на першу позицію рейтингу.
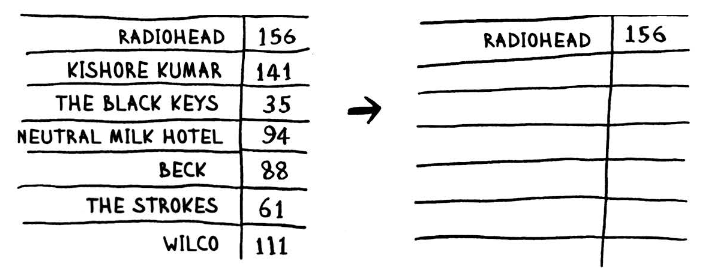
Зі списку видаляємо цей елемент, і у списку, який залишився – шукаємо наступний найбільший і переписуємо у новий список його.
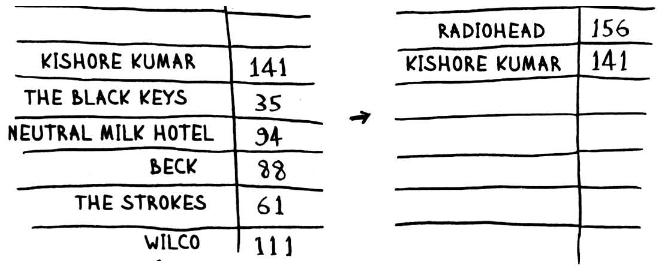
Продовжуючи таким чином, отримуємо упорядкований список:
Спробуймо оцінити цей алгоритм з точки зору ефективності. При простому пошуку (щоразу шукаємо найбільший елемент) – ефективність O, бо до кожного з елементів потрібно звернутись один раз. Цю операцію доведеться робити стільки разів, скільки є елементів у списку, тобто O(n2)
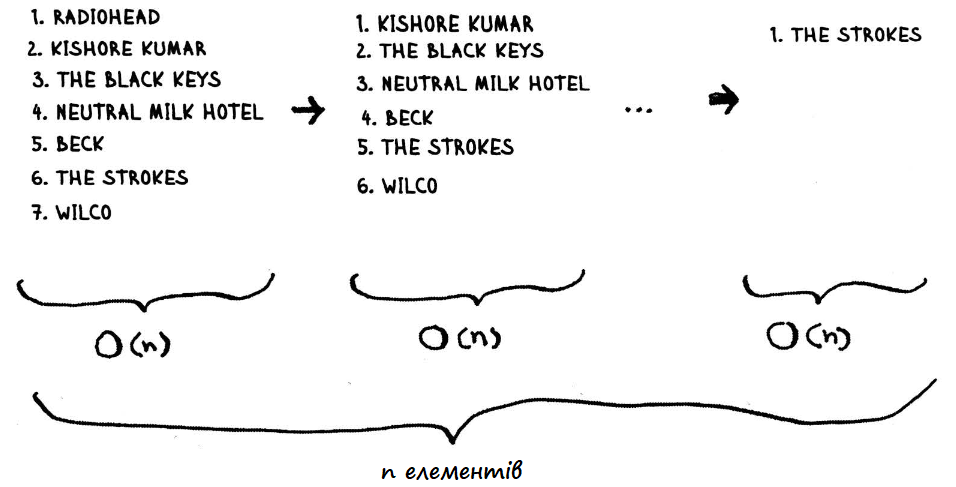
Бачимо, що хоча цей алгоритм дуже легко пояснити, це не найбільш ефективне сортування.
# Знайти найменший елемент у списку
def findSmallest(arr):
# Зберігає значення найменшого елемента
smallest = arr[0]
# Зберігає номер найменшого елемента
smallest_index = 0
for i in range(1, len(arr)):
if arr[i] < smallest:
smallest = arr[i]
smallest_index = i
return smallest_index
# Сортувати список
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
# Шукаємо найменший елемент списку і додає його до нового списку
smallest = findSmallest(arr)
newArr.append(arr.pop(smallest))
return newArr
print selectionSort([5, 3, 6, 2, 10])Швидке сортування O(n log n)
Розглянемо спосіб сортування, який базується на підході «розділяй-і-володарюй». Цей підхід означає, що потрібно вміти розв'язати лише одну базову задачу, а всі решта - намагатись звести до тої, яку вміємо розв'язати. Іншими словами, стратегія зводиться до наступного:
1) Визначається базовий випадок, найпростіший з можливих.
2) Задача ділиться чи скорочується доти, доки не сягне базового випадку.
Базовим випадком буде список, який складається з одного елемента – його не потрібно сортувати. 
Не складно описати сортування списку з двох елементів: порівнюємо два елементи і при потребі – міняємо їх місцями.
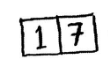
А якщо елементів три?
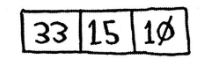
У такому разі беремо перший елемент і ділимо весь список на 2 частини: числа, що менші за цей елемент, і ті, що більші:
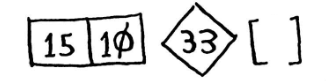
Ці два списки не сортовані, вони просто розділені. Але якби вони були відсортовані, то вони все-одно знаходились би перед цим елементом, або відповідно після нього.
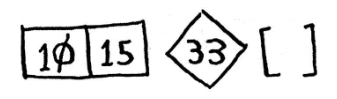
Тобто задача зводиться до того, щоб відсортувати кожен з цих списків. На щастя, перший список складається з двох елементів, а ми вже вміємо сортувати такий список. Таким чином, отримуємо відсортований список.
Якби на першій позиції початкового списку був інший елемент, і він був базовим, то отримали б таку картину:

Знову ж, список відсортовано.
Таким чином, застосовуючи алгоритм сортування лише двох чисел, ми можемо відсортувати довільну кількість чисел! Залишається нагадати, що такий алгоритм називається рекурсією.
def quicksort(array):
if len(array) < 2:
# базовий випадок, список з двох елементів відсортовано
return array
else:
# рекурсія
element = array[0]
# список менших елементів
less = []
for i in array[1:]:
if i <= element:
less.append(i)
# список більших елементів
greater = []
for i in array[1:]:
if i > element:
greater.append(i)
return quicksort(less) + [element] + quicksort(greater)
print (quicksort([10, 5, 2, 3]))
Задача про комівояжера
Цікаво, що за задача про комівояжера? Насправді, це підступно складна задача, у якій мандрівному продавцеві потрібно побудувати оптимальний маршрут переміщення між містами:
Одне із можливих рішень - перебрати всі можливі комбінації порядку відвідування міст, додати відстані між собою і обрати найкращий варіант.
Для 5 міст існує 120 перестановок, тож потрібно буде 120 операцій порівняння. Для 6 міст - це вже 720 можливих перестановок. А для 7 міст - 5040 перестановок. Кількість перестановок стрімко зростає: 8 міст - 40320, 15 міст 1307674368000, 30 міст - 265252859812191058636308480000000. У загальному випадку - кількість операцій становитиме n!
Якщо Ви спробуєте виконати цю задачу для 100+ міст, то на жаль, не встигнете, бо Сонце погасне раніше.
То що ж, ці задачі є безнадійними? Не зовсім, але про це - іншим разом ;)
https://dou.ua/lenta/articles/what-you-should-know-about-algorithms/
