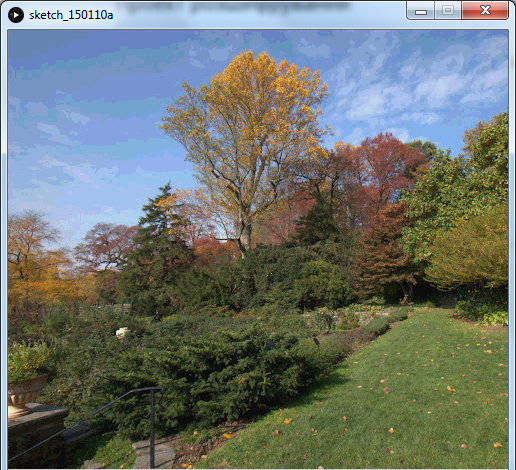
Стеганографія
Шифрування за допомогою прихованих зображень. Наприклад, у древній Греції використовували рабів: на шкірі голови карбувалось таємне повідомлення, котре з часом заростало волоссям. Таким способом можна приховати інформацію, яка ідентифікує автора, комерційну таємницю тощо.
Можна переглянути бітове представлення кольорів пікселів: println(binary(color(255, 0, 255))); отримаємо 11111111111111110000000011111111, що відповідає представленню за схемою AAAAAAAARRRRRRRRGGGGGGGGBBBBBBBB, де спочатку йде альфа-канал (прозорість), а далі три компоненти R/G/B.
Побітні операції, наведені нижче, дозволяють маніпулювати цими значеннями, наприклад для шифрування.
Операція ~ означає логічне заперечення (заміна 0 на 1 і навпаки)
~01010101 =10101010 (~85=170)
Операція & означає логічне ТАК (1, якщо обидва операнди 1)
10001111 & 11011010= 10001010 (143 & 218 = 138)
Операція >> зсув праворуч (зміщує всі біти праворуч
10010111 >> 1 = 11001011 (105 >> 1 = -53)
Операція | означає логічне АБО (1, якщо хоч 1 операнд 1)
10001111 | 11011010 = 11011111 (143 |218 = 223)
Шифрування базується на тому факті, що у представленні кольору різні біти несуть різне змістове навантаження. Так, 4 біти, розміщені ліворуч, несуть більше інформації про колір, ніж 4 біти праворуч. Перші кодують десятки кольорів, тоді як 4 праві біти - лише 16 кольорів, тож спотворення останніх не внесе надто великих змін у зображення.
Видиме зображення:
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
Приховане зображення:
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
Зашифроване зображення (піксель виглядатиме практично як піксель початкового зображення, проте міститиме досить інформації, щоб відновити приховане зображення):
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Проект шифрування
Видиме зображення:

Зображення з прихованим:

Приховане зображення:

Приховане зображення має бути однакового розміру з видимим, і бажано використовувати зображення без великих однотонних областей.
Проект розшифрування
Розшифроване зображення: